An Updated Method for Determining the Rheological Parameters of Composite material

Abstract

The paper discusses the improved methodology for determining the parameters of the influence and relaxation functions of composite materials with elastic-plastic properties, on the example of nonlinear deformation. The approach is based on the so-called on the application of the heredity theory. Due to the existence of a complex mathematical apparatus, the parameters of the rheological functions of the material 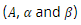today, it is determined by combining theoretical and experimental graphs [1, 2].

This method is outdated and associated with certain inaccuracies. In particular, the determination of the strength characteristics of a specific material and the coefficient of theoretical and experimental time displacement gives a significant error during further calculations. In the presented improved method, parameters of material influence and relaxation functions 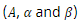the selection for the given phase of the research is done using the existing methodology, based on the simple similarity (combination) of the graphs of the functions. Also, subsequently, theoretical and experimental curves are approximated to a polynomial of any degree, using the least squares method. In the example discussed below, approximations are made to 4th and 7th degree polynomials. In the corresponding polynomial expansion of the theoretical curve, based on the consideration of greater smoothness of the graph of the function, two additional parameters are calculated, which ensure the displacement of this curve on the horizontal and vertical axes, which should coincide as much as possible with the corresponding graph of the experimental polynomial.

The mentioned parameters will be determined by a procedure similar to the least squares method. In particular, the sum of the squares of the differences between the theoretical and experimental values at specific points of the functions arguments should be minimal. The task of finding the minimum of a function of two variables should be solved. The corresponding calculations are made using the computer program "Maple" and the corresponding solutions are obtained. Based on a specific example, the results
obtained by the existing and improved method are compared.